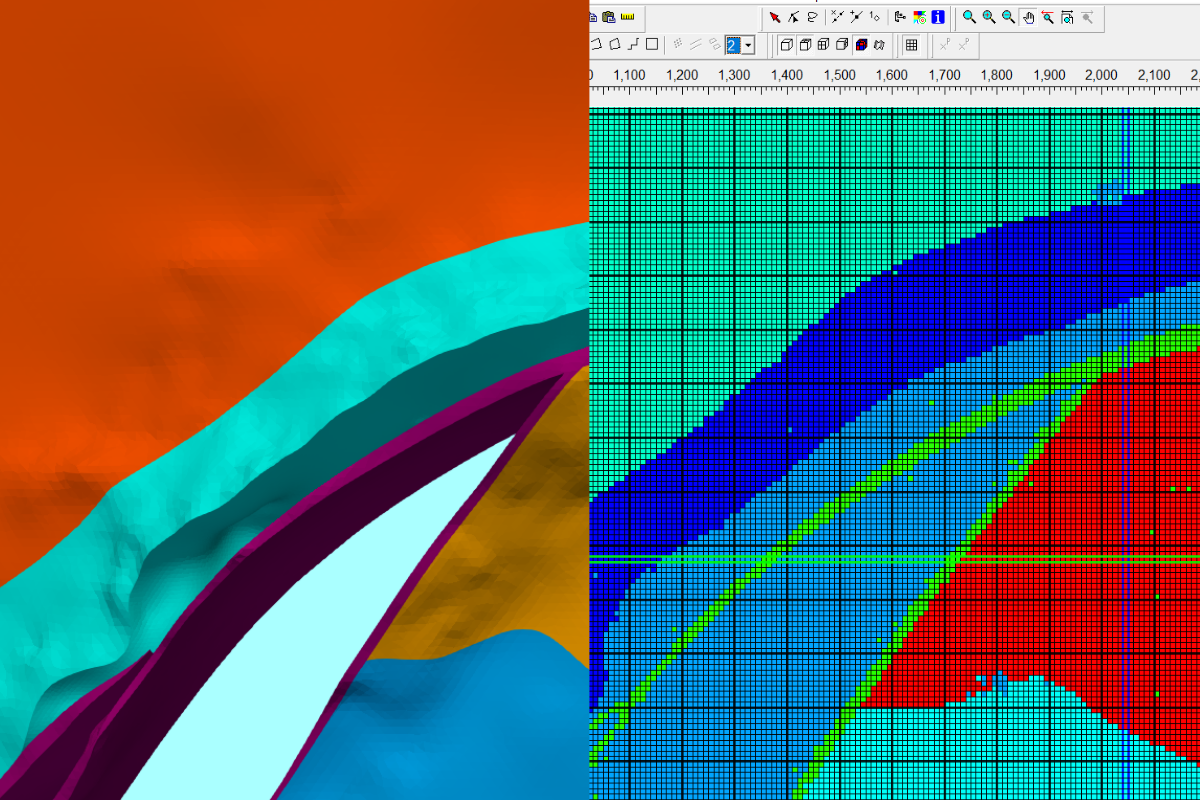
Desde que un acuífero homogéneo fue modelado, existe un interés en comparar los resultados con una solución analítica. Algunas fórmulas dan el valor de reducción en el pozo para un flujo estable en acuíferos, confinados y no confinados, homogéneos, isotrópicos e infinitos en la extensión horizontal con un solo pozo de penetración.
Desarrollo del cono de depresión de un pozo y su interacción con un curso de agua.
Esas fórmulas son [Braun, Färber, 2004]:
Caso Confinado:
Caso No Confinado:
Donde:
sw : Reducción en el perímetro exterior del pozo filtrante
Qo : Tasa de bombeo
ho : Espesor del acuífero saturado sin perturbación
m : Altura del acuífero confinado
rw : Radio del pozo
K : Conductividad hidráulica
R : Radio de influencia
Todos los parámetros mencionados arriba fueron definidos en la conceptualización del modelo, excepto los valores del "Radio del pozo" y del "Radio de Influencia". El radio del pozo puede ser estimado a partir de un pozo encamisetado estándar, pero el radio de influencia tiene que ser determinado con la ayuda de algunas fórmulas.
El "Radio de Influencia" está definido como la máxima distancia en la cual las reducciones pueden ser detectadas con los instrumentos de medición usuales en el campo [Dragoni, 1998]. Debido a las herramientas numéricas, el concepto de "Radio de Influencia" es de uso limitado en la actualidad [Dragoni, 1998].
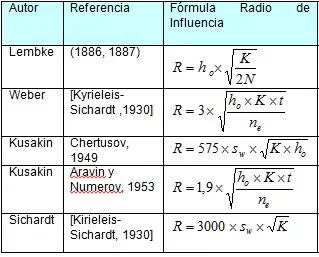
La manera más común de encontrar el "Radio de Influencia" es el uso de fórmulas empíricas. Estas fórmulas se encuentran listadas abajo.
Con:
N = Recarga de agua subterránea
ho = Espesor del acuífero saturado
K = Conductividad hidráulica
ne = Porosidad efectiva
sw = Reducción en el perímetro exterior del pozo
t = Tiempo
Algunas fórmulas requieren otros parámetros (recarga, porosidad efectiva y tiempo de bombeo). Es interesante mencionar que ninguna de estas fórmulas usa la tasa de bombeo como parámetro para hacer los cálculos.
Es también posible estimar el radio de influencia, o en particular, el área de influencia de un cono de depresión como el área donde la reducción excede 1 pie (30,48 cm.) [Myette, Olimpio, Johnson, 1987].
La fórmula más común para determinar el radio de influencia es la fórmula de Sichardt, aunque el valor de radio para esta fórmula es la más pequeña y representa el 40 % de la máxima reducción. Por lo tanto, el valor de radio de Sichardt no encaja con la definición de radio de influencia. Situaciones similares ocurren para ambas fórmulas Kusakin.
La dispersión de los valores del radio de influencia muestran la naturaleza empírica de las fórmulas, la cual sólo depende de los parámetros considerados.
Referencias
- Dragoni W.: Some consideration regarding the radius of influence of a pumping well. Perugia Italy, 1998. Web:http://www.unipq.it/~denz/Dragoni.pdf
- Kyrieleis, W., Sichardt, W. – Grundwasserabsenkung bei Fundierungsarbeiten, Springer, Berlin, 1930
- Myette, C., Olimpio, J., Johnson, D.- Area of Influence and Zone of Contribution to Superfund Site Wells G & H Woburn, Massachusetts, U.S. Geological Survey, USA, 1987. Web: http://www.civil-action.com/facts/keydocuments/usgsrpt.html