Para la comprensión del ciclo hídrico a escala regional en cuencas no medidas se requieren de herramientas que relacionen valores de precipitación con otras variables como latitud, longitud y elevación.
El método del vector regional es muy práctico porque te permite tener una fórmula que relaciona posición y elevación con la precipitación en cualquier parte de la cuenca, tomando como referencia valores observados. El vector regional puede ser univariado o polivariado, pero siempre es lineal.
Para una zona de estudio, tomando en cuenta estas tres variables, el vector regional sería expresado de esta manera:
Precipitación = Factor1 x Longitud + Factor2 x Latitud + Factor 3 x Elevación + Coeficiente
Este artículo muestra como se puede generar el vector regional con Python y el paquete scikit-learn.
Datos de entrada
Para la realización de esta correlación se utilizaron 8 estaciones distribuidas en 3 países como se muestra en la figura a continuación:
Distribución de las estaciones en la zona de estudio.
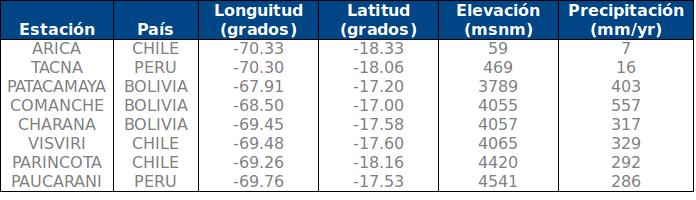
Las estaciones utilizadas estaban a elevaciones que iban desde los 59 msnm hasta los 4541 msnm. Los datos de precipitacion, elevación y ubicación de las estaciones se muestra a continuación.
Datos de las estaciones utilizadas.
Cuando la correlación precipitación elevación no es suficiente
Muchos vectores regionales de precipitación regional solo consideran la relacion lineal de precipitación con elevación. Esto puede ser práctico para cuencas entre 60 km2 a 180 km2. Si estamos tratando con escalas regionales mayores a 10000 km2 entonces otros factores como la latitud y longitud pueden tener una mayor influencia en la precipitación.
A continuación vemos un gráfico donde se muestra que la relación lineal y directa entre precipitación - elevación para un área de estudio de 74 000 km2 ya no se cumple. La precipitación sube con la elevación hasta cotas menores a 4000m, luego disminuyen a medida que sube la elevación.
Finalmente el código
Y por último, se muestra el código en Python que realiza la regresión multilineal que corelaciona la latitud, longitud y elevación con la precipitación.
from sklearn import linear_model
from numpy import genfromtxt
### importamos los datos como un elemento de numpy
mis_datos = genfromtxt('Variables_Climaticas.csv', delimiter=',')
mis_datos_corr = mis_datos[1:,:]
mis_datos_corr
### generamos la correlacion lineal con LinearRegresion
clf = linear_model.LinearRegression()
clf.fit(mis_datos_corr[:,1:],mis_datos_corr[:,:1])
### imprimimos los coeficientes
clf.coef_
### imprimimos el factor independiente
clf.intercept_
### vemos los valores predecidos con a correlacion
clf.predict(mis_datos_corr[:,1:])
Corriendo este código podemos llegar a la siguiente ecuación del vector regional:
Precipitación (mm/año) = 38.14 x Longitud° + 235.78 x Latitud° + 0.03887 x Elevación (msnm) + 6975.33
Vea el código y los archivos asociados en nuestro perfil de github: