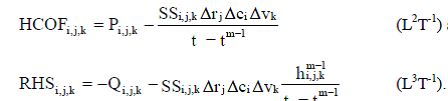MODFLOW emplea métodos iterativos para obtener la solución del sistema de ecuaciones en diferencias finitas para cada intervalo de tiempo. El proceso de iteración se inicia asignado la carga con un valor arbitrario en cada nodo. Al alterar estos valores estimados se produce un nuevo conjunto de valores de carga hidráulica que entran nuevamente al sistema de ecuaciones. Estos nuevos valores de carga hidráulica toman el lugar de los valores asignados a las cargas iniciales y el procedimiento de cálculo se repite y genera un tercer conjunto de cargas. Este procedimiento se repite sucesivamente en cada etapa, produciendo nuevos valores provisionales de carga que satisfacen al sistema de ecuaciones. Cada repetición del cálculo se denomina una “iteración”. Por último las cargas hidráulicas generadas en las iteraciones deben acercarse a valores que satisfagan al sistema de ecuaciones, y los cambios en las cargas hidráulicas de cada iteración deben tener valores muy pequeños. Este comportamiento se utiliza para determinar en qué momento se debe detener la iteración.
Durante los cálculos en un intervalo de tiempo, las matrices de valores de carga hidráulicas intermedias se generan en la sucesión de iteraciones. Cada matriz tiene un valor de carga intermedia para cada nodo activo en la malla o grilla. En la figura 2-6 las matrices son representadas en tres dimensiones, cada una identificada por un símbolo de matriz, h, con dos exponentes. El primer súper índice indica el intervalo de tiempo para que las cargas se calculen mientras que el segundo súper índice indica el número o nivel de la iteración que género nuevos valores de carga.
Figura 2-6. Calculo iterativo de una distribución de carga hidráulica ( de McDonald and Harbaugh, 1988.)
En condiciones ideales, uno mismo quisiera especificar en qué momento detener la iteración cuando las cargas estén calculadas muy cerca de la solución exacta. Dado que la solución real se desconoce, se requiere un método directo de especificar cuándo se debe detener la iteración. El método más empleado para especificar los cambios de carga hidráulica calculado consiste en designar un cambio en las cargas hidráulicas que debe ser menor que una cierta cantidad desde una iteración a la siguiente. Este valor en las variaciones de las cargas hidráulicas calculadas se llama “Criterio de Cierre” ó “Criterio de convergencia”, este criterio es definido por el usuario.
Una vez realizada la iteración, los valores de las cargas hidráulica calculadas son examinadas en cada nodo de la malla para compararlos con el criterio de convergencia, en caso que el valor de la carga hidráulica sea excedido por el criterio de convergencia, la iteración continua, en caso contrario cuando el valor de carga hidráulica generado es menor que el criterio de convergencia, la iteración para el intervalo de tiempo se detiene y se dice que esta “cerrada” o es “Convergente”. Como regla general se aconseja que utilizar un criterio de valor de cierre de un orden de magnitud menor que el nivel de precisión deseada en los resultados de la carga.
Simulación del Estado Estacionario
La ecuación 2-6 corresponde a la ecuación de flujo y se desarrolló suponiendo condiciones transitorias. Sin embargo, la ecuación de flujo transitorio se convirtió en la ecuación de flujo estacionario cuando el valor del almacenamiento es cero. La ecuación resultante enuncia que la suma de la salida de todos los flujos de las celdas adyacentes y los requerimientos externos deber ser cero para cada celda en el modelo. Un problema en estado estacionario requiere solamente una única solución de ecuaciones simultáneas, en lugar de múltiples soluciones para intervalos de tiempo múltiples como es el caso del estado transitorio.
Ec.2-6
Formulación de ecuaciones para la solución
MODFLOW incorpora varias opciones para realizar la solución iterativa del conjunto de ecuaciones en diferencias finitas. Se organizan estas opciones de tal manera que los esquemas alternativos de solución se pueden añadir sin alterar la estructura del programa.
Cualquier esquema de solución que se emplee, es conveniente para reorganizar la ecuación 2-6. Todos los términos que contengan a la carga hidráulica al final del proceso se agrupan del lado izquierdo de la ecuación y todos los términos que son independientes a la carga al final del proceso son agrupados en el lado derecho de la ecuación. Todos los coeficientes en hmi, j,k que no incluyen las conductancia entre nodos son combinados en un solo termino, HCOF, y todo los términos del lado derecho se combinan. Además, la complejidad se puede reducir si se asume que el tiempo es m a menos que se indique lo contrario, por lo tanto la ecuación resultante es:
(2-7)
Donde:
El tipo de celdas y simulación de fronteras
En la práctica la formulación de la ecuación 2-7, para cada celda en un modelo de malla es generalmente innecesario, por que el estado de ciertas celdas se especifica previamente para simular las condiciones de borde o frontera.
En MODFLOW, las celdas empleadas para simular las condiciones de borde o frontera se agrupan en dos categorías, celdas con “Carga constante” y celdas “no flujo”. Las celdas con carga constante son aquellas en las cuales se especifica la carga hidráulica cada vez, y el valor de la altura no cambia como resultado de la solución a la ecuación de flujo.
Las celdas declaradas como “no flujo”, son aquellas que en las que no hay flujo dentro o fuera de la celda. Las celdas restantes de la malla o grilla denominadas “Variables” son caracterizadas por tener una carga hidráulica no especificada y pueden variar libremente con el tiempo.
Aspectos conceptuales de discretización vertical
MODFLOW maneja la discretización espacial en la dirección horizontal en filas y columnas donde cada columna y fila tienen un ancho definido. La discretización espacial en la dirección vertical es manejada especificando el número de capas que serán utilizadas, y especificando las elevaciones superior e inferior de cada capa.
De un lado, la discretización vertical puede ser simplemente visualizada como una extensión de la discretización aérea en un proceso más o menos arbitrario de dividir el sistema de flujo en segmentos en la dimensión vertical gobernado en parte por la resolución vertical deseada en los resultados. De otro lado. La discretización vertical puede ser vista como un esfuerzo para representar los acuíferos o las capas permeables.
Cada uno de estos métodos para visualizar el proceso de discretización vertical tiene ventajas, así como dificultades.
Las ecuaciones del modelo se basan en la suposición de que las propiedades hidráulicas son uniformes dentro de cada celda, o al menos que el promedio o las propiedades integradas pueden ser especificados para cada celda. Estas condiciones son más probables de ser cumplidas cuando las capas del modelo están conformadas de acuerdo a las unidades hidrogeológicas.
Los enfoques de la discretización vertical descritos anteriormente conducen a un conjunto de ecuaciones de la forma de la ecuación 2-7, que deben ser resueltos de forma simultánea en cada intervalo de tiempo.
Las diferencias entre estos enfoques surgen de la manera en que las conductancias y condiciones de almacenamiento son formuladas, en el número de ecuaciones a ser resuelta, en la resolución de resultados y en la precisión de los resultados. MODFLOW es capaz de implementar cualquiera de estos enfoques de discretización vertical en que las elevaciones de las celdas individuales de cada capa pueden variar.