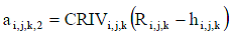El movimiento en tres dimensiones del agua subterránea de densidad constante, a través del medio poroso en el suelo, puede ser descrito por la ecuación diferencial parcial:
(2-1)
Donde Kxx, Kyy, y Kzz son los valores de la conductividad hidráulica en a lo largo de los ejes x, y, z los cuales se asumen paralelos a los ejes principales de la conductividad hidráulica (L/T);
h es la carga Hidráulica (L);
W es el flujo volumétrico por unidad de volumen representada por las fuentes y/o sumideros de agua, con W<0.0 para el flujo entrante al sistema (T-1);
SS es el almacenamiento especifico del material poroso (L-1), y t es el tiempo (T)
La ecuación 2-1 describe el flujo de agua subterránea bajo condiciones de no equilibrio en un medio heterogéneo anisótropico siempre que los ejes principales de conductividad hidráulica estén alienados con la dirección de las coordenadas.
La ecuación 2-1 con la especificación del flujo y/o las condiciones de carga hidráulica, los límites del acuífero y especificando las condiciones iniciales de carga hidráulica, constituye una representación matemática del flujo de agua subterránea.
Convención de Discretización
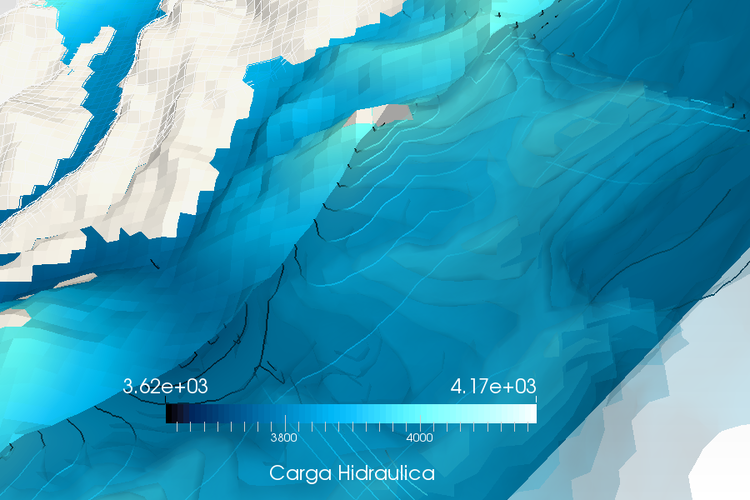
En la Figura 2-1 se muestra una discretización espacial de un acuífero con una malla de bloques llamadas celdas, las localizaciones de cada una se describen en términos de filas, columnas y capas. Se emplean en el sistema los subíndices i, j, k.
Para un sistema de “NROW” filas, “NCOL” columnas y “NLAY” capas, i es la fila indexada, i = 1,2,… NROW; j es la columna indexada, j = 1,2,… NROW; y k es la capa indexada, k = 1,2,… NLAY. Por ejemplo, la figura muestra un sistema con 5 filas, NROW = 5, 9 filas NCOL = 9, y 5 capas NLAY = 5.
En la formulación de la ecuación del modelo, se puede suponer que las capas generalmente corresponden a los intervalos o unidades hidrogeológicas horizontales. En términos de coordenadas cartesianas, el índice k denota los cambios a lo largo de la vertical, z. Debido a la convención en el modelo matemático el numero de capas se enumera de arriba hacia abajo, un incremento en el índice k corresponde a una mayor profundidad. De manera similar las filas pueden ser consideradas paralelas al eje x, por lo tanto el incremento en el índice, i, de las filas corresponde a la disminución en el eje. Las comunas pueden considerarse paralelas al eje x, entonces, el incremento en el índice, j, corresponde al incremento en el eje x. Con esta convención fue construida la Figura 2-1, sin embargo, las aplicaciones del modelo sólo requieren que las filas y las columnas sigan direcciones ortogonales coherentes dentro de las capas y esto no requiere la asignación de los ejes coordenados x, y, z.
Dentro de cada celda existe un punto llamado “Nodo” en el cual se calcula la carga hidráulica. Existen muchos sistemas para localizar los nodos, sin embargo, la ecuación de diferencias finitas utiliza la formulación de bloque centrado (BCF package), esto quiere decir que supone que los nodos están al centro de la celda.
Siguiendo la convención del la Figura 2-1, el ancho de las celdas en la dirección de las filas y dada la columna, j, es designado por Δrj; el ancho de la celda in la dirección de las columnas está dada por la fila, i, es designada por ΔCi; y el espesor de la celda en una capa dada, k, se asigna ΔVk. Por lo tanto, una celda con coordenadas i, j , k = (4,8,3) tiene un volumen de Δr8ΔC4ΔV3.
En la ecuación 2-1, la carga hidráulica, h, es una función del espacio y tiempo. En la formulación de la ecuación de diferencias finitas la discretización del tiempo también es necesaria. El tiempo se divide en intervalos de tiempo y la carga hidráulica es calculada en cada intervalo de tiempo.111
Figura 2-1. Una discretización hipotética del sistema acuífero (Modificada de McDonald and Harbaugh, 1988.)
Ecuación de diferencias finitas
El desarrollo de la ecuación del flujo de agua subterránea con la ecuación de diferencias finitas está basado en la ecuación de continuidad: “la suma de todos los flujos de entrada y salida en la celda debe ser igual al cambio en el almacenamiento dentro de la celda”. Considerando que la densidad del agua en el suelo es constante, la ecuación de continuidad se expresa de la siguiente manera para cada celda:
(2-2)
Donde:
Qi es el flujo en la celda (L3T-1);
SS fue introducida a para hacer una anotación especifica en la ecuación de diferencias finitas, esta definición es equivalente a Ss en la ecuación 2-1, entonces SS es el volumen de agua que puede ser introducido por unidad de volumen del material de un acuífero por unidad de cambio en la carga hidráulica (L-1);
ΔV es el diferencial de volumen de la celda (L3); y
V es el volumen de la celda (L3); y
Δh es el cambio de la carga hidráulica en un intervalo de tiempo.
El término del lado derecho de la ecuación es equivalente al volumen de agua que se puede tomar del almacenamiento sobre un intervalo de tiempo Δt debido al cambio en la carga Δh. La ecuación 2-2 está en términos de entrada de flujo y almacenamiento. Los flujos de salida y las pérdidas están representadas de la siguiente manera: el flujo de salida como un flujo de entrada negativo y las pérdidas como una ganancia negativa.
Figura 2-2. Índices para las seis celdas adyacentes que rodean a la celda i, j, k (oculta). (Modificada de McDonald and Harbaugh, 1988.)
La figura 2-2 muestra 6 celdas del acuífero adyacentes a la celda i, j, k-1, j, k, i+1, j, k, i, j-1, j, i, j-1, k, i , j+1, k, i, j, k-1, y i, j, k+1. Los flujos son considerados positivos si están entrando en la celda i, j, k; el signo negativo usualmente incorporado en la ley de Darcy se ha eliminado de todos los términos. Siguiendo esta convención, el flujo de entrada en la celda i, j, k en la dirección de la fila de la celda i, j-1, k (Figura 2-3) está dada por la ley de Darcy como:
Donde:
h i, j, k es la carga en el nodo i, j, k y h i, j-1, k es la carga en el nodo i, j-1, k;
q i,j-1/2, k es el rango de flujo volumétrico entre las caras de las celdas i, j, k y i, j-1, k(L3 T-1);
KR i, j-1/2, k es la conductividad hidráulica a lo largo de la fina entre los nodos i, j, k y i, j-1, k (LT-1);
ΔCiΔVk es el área de la superficie normal de la celda en la dirección de la fila; y
Δrj-1/2 es la distancia entre los nodos, i, j, k y i, j-1, k(L).
El subíndice i, j-1/2 que se utiliza en la ecuación 3, para designar la región entre nodos i, j-1, k e i, j, k. El “1/2” no indica una forma, específica un punto medio entre los nodos. Así, Qi, j-1/2, k indica que el flujo desde el nodo i, j-1, k hacia el nodo i, j, k, Δrj-1/2 es la distancia entre el nodo i, j, k y el nodo i, j -1/2, k, KR i, j-1/2, k es la eficiencia de la conductividad hidráulica entre los nodos. El término “1/2” se utiliza de la misma manera para indicar la región entre nodos.
Figura 2-3. Flujo en la celda i, j, k desde la celda i, j-1, k. (Modificada de McDonald and Harbaugh, 1988.)
La ecuación 2-3 da el flujo exacto para una dimensión en flujo estacionario.
Por ejemplo, supongamos que una celda está recibiendo un flujo de dos fuentes, la recarga de un pozo y la infiltración a través de del cauce de un río. Para la primera fuente (n = 1), porque el flujo del pozo se supone que es independiente de la carga hidráulica, pi, j, k, 1 es cero y el qi, j, k, 1 es la velocidad de recarga en el pozo. En este caso se tiene:
(2-4)
Para la segunda fuente (n = 2), se hace la hipótesis de que la interconexión río-acuífero puede ser tratada como una conductancia simple, por lo que la infiltración es proporcional a la diferencia entre el nivel de la carga hidráulica en el río y la carga hidráulica en la celda i, j, k (Figura 2-4), por lo tanto se tiene la siguiente expresión:
Donde:
R i, j, k es la carga hidráulica en el río, y
CRIV i, j, k es una conductancia que controla el flujo del río dentro de la celda i, j, k.
Figura 2-4. Modelo conceptual del cauce de un río en una celda (Modificado de McDonald y Harbaugh, 1988.)
La aproximación para la derivada en diferencias finitas respecto al tiempo de la carga hidráulica, Δhi, j, k / Δt debe ser expresada en términos de carga hidráulica especifica y tiempos. La Figura 2-5 muestra un hidrograma de valores de la carga hidráulica en el nodo i, j, k. Dos valores de tiempo se muestra en el eje horizontal: tm, el tiempo en que los términos de flujo de la ecuación (2-23) se evalúan, y tm-1, un tiempo que precede tm. Los valores de carga hidráulica en el nodo i, j, k asociado a estos tiempos son definidos por el superíndice como hm i, j, k y hm-1i, j, k, respectivamente. Una aproximación a la derivada respecto al tiempo de la carga hidráulica en el tiempo tm se obtiene dividiendo la carga hidráulica en diferencia hm-1i, j, k - hmi, j, k por el intervalo de tiempo tm- tm-1, es decir:
Por la tanto, la pendiente del hidrograma, o derivada respecto al tiempo, es una aproximación utilizando el cambio en la carga hidráulica en el nodo de más de una vez intervalo de tiempo que precede, y termina con el tiempo en que el flujo es evaluado. Esto se denomina una diferencia hacia atrás, en que Δh/Δt se aproxima más de un intervalo de tiempo que se extiende hacia atrás en el tiempo desde tm, el tiempo en que los términos de flujo se calcularon.
Figura 2-5. Hidrograma para la celda i, j, k.
Explicación
tm Tiempo de fin del intervalo de tiempo m.
hm i, j, k Carga hidráulica en el nodo i, j, k del tiempo tm.
Aproximación de la diferencia hacia atrás de la pendiente del hidrograma en el tiempo tm.
El conjunto de ecuaciones en diferencias finitas es reformulada en cada intervalo del tiempo, es decir que en cada intervalo de tiempo hay un nuevo sistema de ecuaciones múltiples que hay que resolver.
Las cargas hidráulicas son las incógnitas de este proceso para que el sistema de agua subterránea tenga solución; las cargas hidráulicas al inicio del cálculo son términos conocidos en la ecuación.
El proceso de solución se efectúa en cada intervalo de tiempo el cual tiene por resultado una nueva matriz de cargas hasta completar el final de la etapa.
La ecuación de flujo en diferencias finitas para cada celda es una representación del flujo volumétrico fijo de todas las fuentes en unidades de L3/T (donde L es una unidad de longitud y T es una unidad de tiempo). El uso de unidades deber especificarse y deben ser consistente ya que el uso incorrecto de unidades no puede ser detectado.